What Is The Formula To Find The Volume Of A Sphere?

Permit'southward larn how to make up one's mind thevolume of a sphere.

What is a Sphere?

A sphere is a perfectly symmetrical three-dimensional shape whose all surface points are equidistant from the center. The altitude from the center to any point on the surface is called the radius. Twice the radius is the diameter or the line segment that passes through the heart. Examples of sphere-shaped objects are marbles, bubbles, and balls.

How to find the Volume of a Sphere

The book of a sphere is four-thirds of the product of pi and radius cubed, as expressed in this formula:

V = (4/3)πr^three
where π = 3.14 and r = radius

Like other three-dimensional shapes, the volume of a sphere is measured in cubic units such equally cubic inch (in³), cubic feet (ftⁱⁱⁱ), cubic centimeter (cm^three), or cubic meter (grand³).

Here's a quick guide to finding a sphere's volume:

Step ane. Write down the given figures. You'll need the radius or the bore. Brand sure all measurement units are the same. If not, convert either of them.

Footstep 2. Plug the figures into the formula.

Step 3. Perform the operations: multiplication and division. Don't forget to write the cubit unit together with the reply.

Related Reading: Volume of a Cylinder – Formula & Examples

Example 1: Finding the Volume of a Sphere when given the Radius

Find the volume of the sphere below.

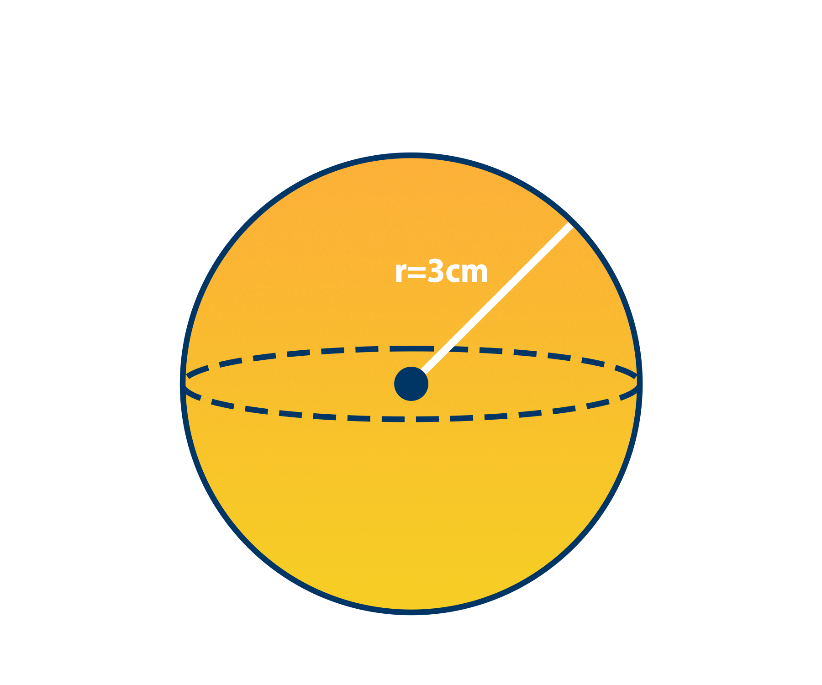
Solution for Example 1:

Write down the given figure, which is the radius (r = 3cm).

Substitute 3cm for r into the formula.

5=(iv/3)πr³

5=(iv/3)π(3cm)³

Simplify.

5=(4/three)π(27cm³)

V=113.09cm³…

Therefore, the book is about 113.09cm³ .

Instance 2: Finding the Book of a Sphere when given the Diameter

Find the volume of the sphere below.

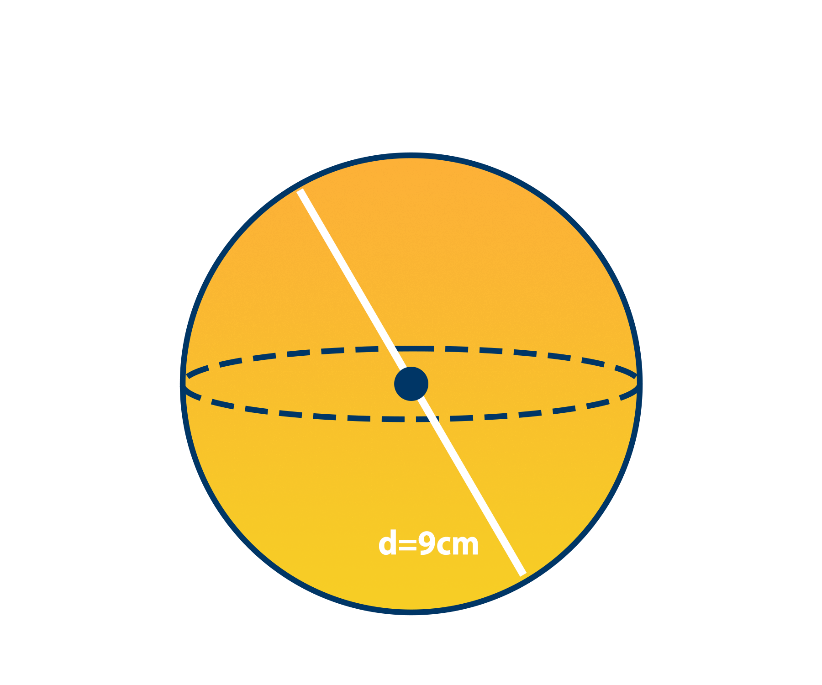
Solution for Example 2:

Write downwardly the given figure, which is the diameter (d = 9cm). Since a sphere's volume formula requires the value of the radius, find the radius.

You may recollect that diameter is twice the radius. So, split up the diameter (d = 9cm) past 2 to obtain the radius.

r = d/2 = 9cm/two = 4.5cm

Substitute four.5cm for r in the equation.

5=(4/3)πr³

Five=(4/iii)π(iv.5cm)³

Simplify.

V=(iv/three)π(91.125cm³)

V = 381.70cm³…

Therefore, the book is nearly 381.70cm³ .

Thank yous for reading. We hope it's effective! E'er feel free to revisit this folio if you ever have any questions almost thevolume of a sphere.